>

Operations Research •

Traveling Salesman Optimization

Project developed during the Operations Research 2 course in the academic year 2023/24. The aim of the project is to explore different approaches for solving the famous Travelling Salesman Problem (TSP), ranging from very approximate solutions with heuristic algorithms down to exact methods employing CPLEX MIP solver.

Client

University

Technologies

C, Cplex, Make, Gnuplot

Open Project →

The Traveling Salesman Problem (TSP) stands as one of the most renowned and extensively studied combinatorial optimization challenges in the realm of computer science, operations research, and applied mathematics. At its core, the TSP revolves around finding the shortest possible route that a salesman must take to visit a given set of cities exactly once and then return to the original city. Despite its seemingly straightforward premise, the TSP’s complexity escalates rapidly as the number of cities increases, leading to its classification as an NP-hard problem.

During the course we explored and implemented the following algorithms:

  • Heuristics
    • Nearest Neighbour
    • All Nearest Neighbour
    • All Nearest Neighbour + 2-OPT
    • Extra Mileage
  • Meta-Heuristics
    • Tabu Search
    • Variable Neighborhood Search
  • Exact Methods
    • Benders Loop
    • Benders Loop with Patching
    • Branch & Cut
  • Math-Heuristics
    • Hard Fixing
    • Local Branching

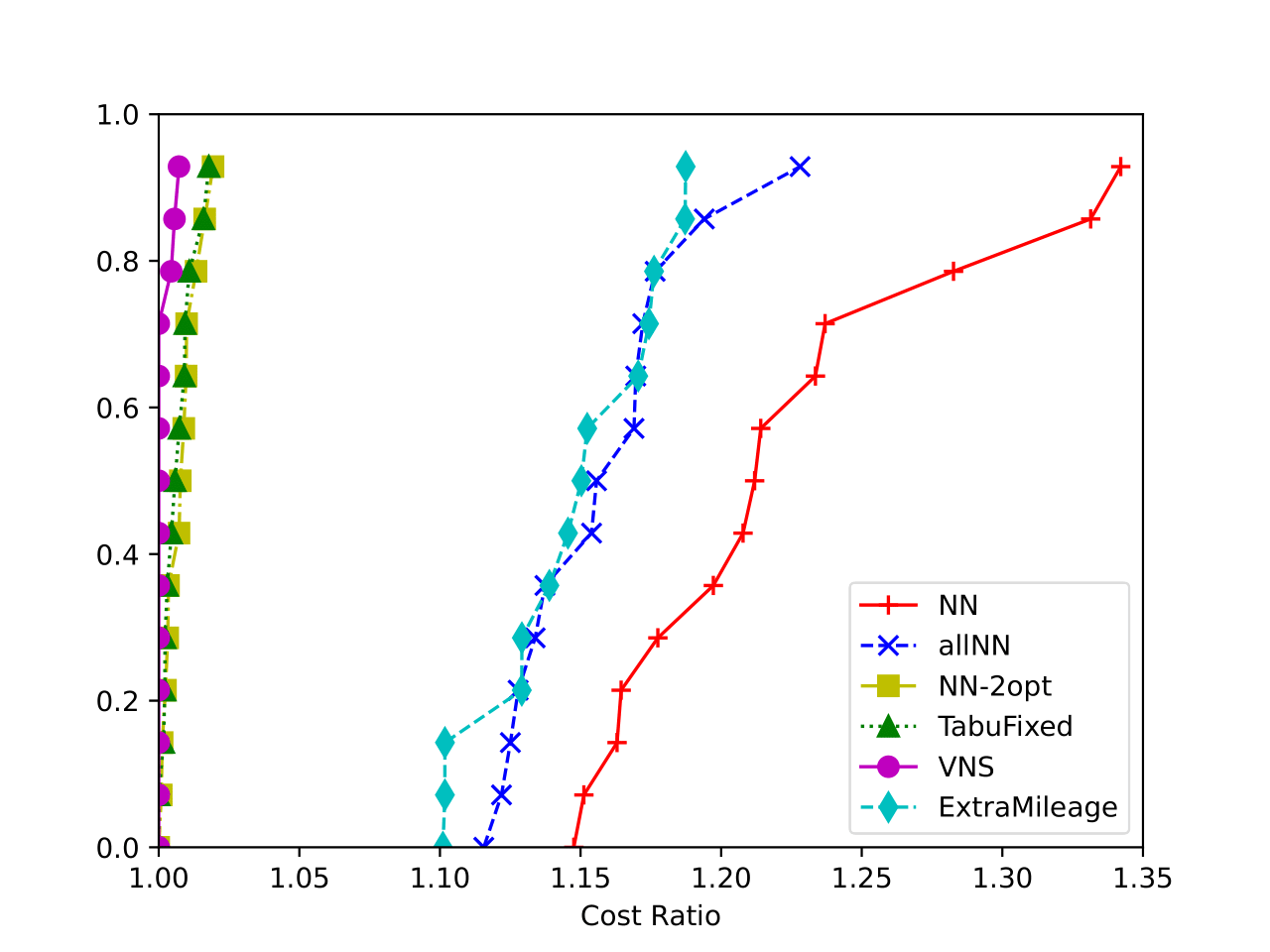
Heuristics perform exceptionally well with 2000 nodes, whereas exact models struggle even with 400 nodes. However, this speed advantage comes with a trade-off: the best metaheuristic (VNS) has a gap of less than 4% from the optimal solution. Heuristics Results For exact solutions, the best choice, in terms of the time to reach the optimal solution, is Branch&Cut with fractional cuts and a heuristic initial solution. 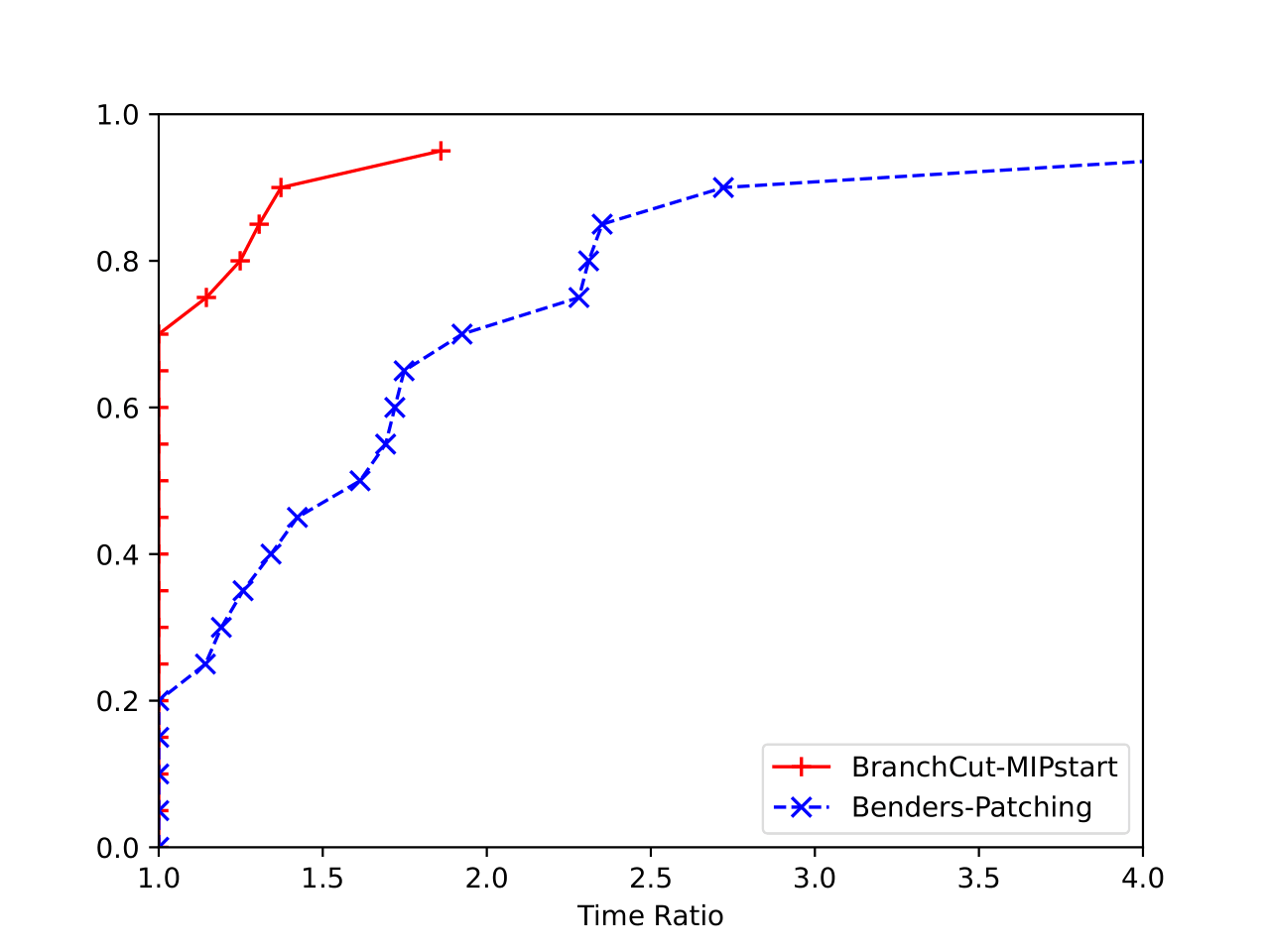Exact Results Matheuristics are effective when exact models cannot find the optimal solution within a feasible time limit, enabling us to solve instances with more nodes by leveraging the CPLEX mathematical model. The best performing matheuristic is Hard Fixing, though it has a small gap compared to Local Branching. Meta-Heuristics Results Further results, including hyper-parameters tuning, can be found in the project report.