Curse of Dimensionality in the KNN problem

Select Connection: INPUT[inlineListSuggester(optionQuery(#permanent_note), optionQuery(#literature_note), optionQuery(#fleeting_note)):connections]

The term curse of dimensionality was introduced in 1961 by Bellman. Nowadays it is a general term related to high dimensional data, spanning in different domains like machine learning, data mining and obviously the k Nearest Neighbor problem. In this context, it refers to the exponential dependency of both space and time on the number of dimensions. A key reason for this inefficiency is related to the distance concentration, a phenomenon where in high dimensions the distances between all pairs of points have almost the same value. To illustrate the effect, consider the example in Figure \ref{}. 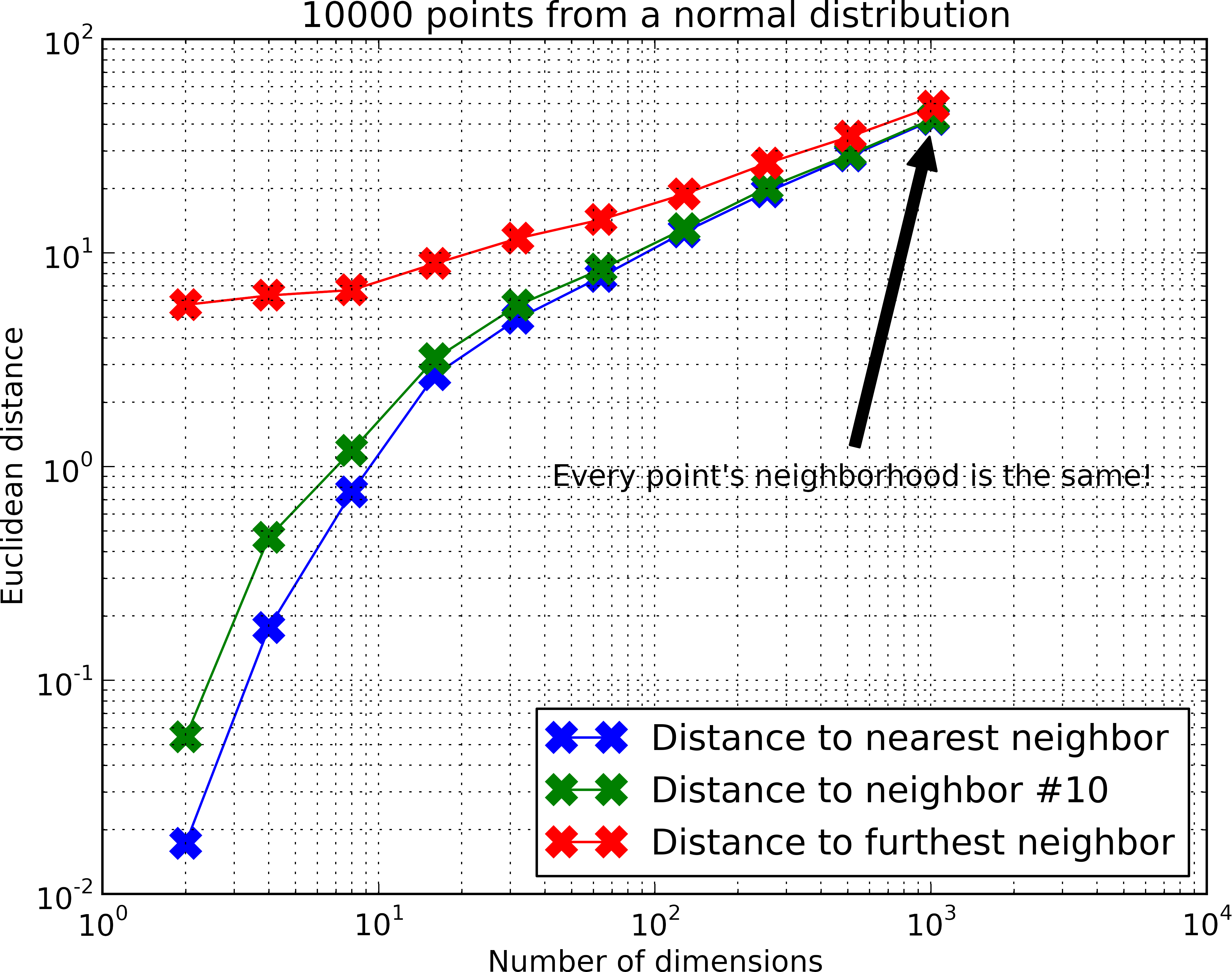As the number of dimensions increase, the relative difference between the closest and farthest points becomes increasingly negligible, so it’s exponentially more difficult to distinguish true nearest neighbors. This effect is captured by the relation in Equation \ref{}.

$$\underset{d\to \infty }{\lim }E\left(\frac{{\text{dist}}_{max}(d)-{\text{dist}}_{min}(d)}{{\text{dist}}_{min}(d)}\right)\to 0$$

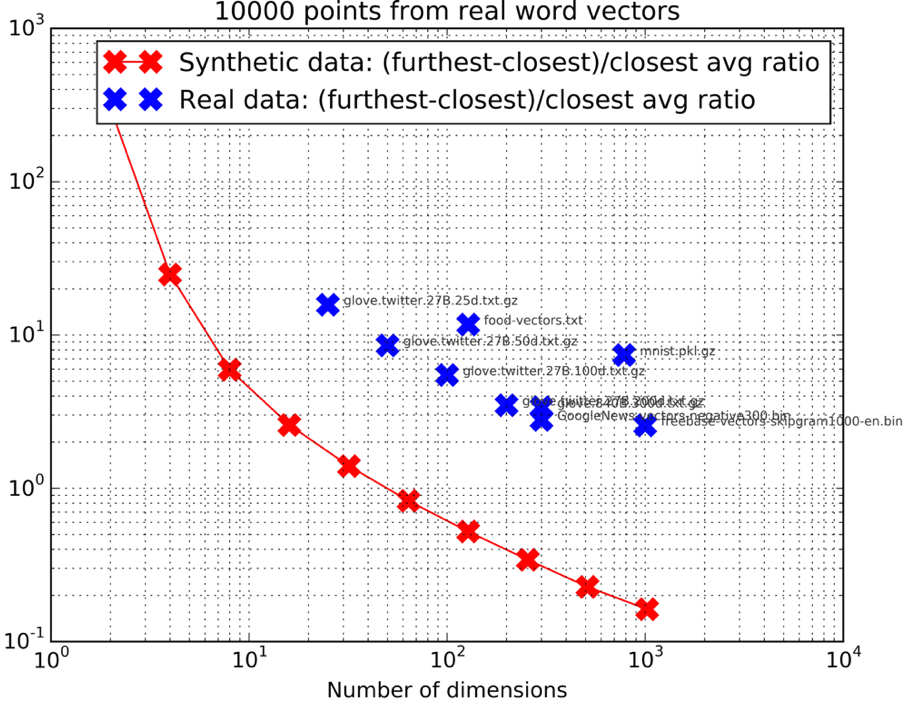
This rule applies in datasets generated from distributions where there is little to no structure, like the Normal distribution in the example. However, in real-world datasets, data often has significant structure, meaning that while the explicit dimensionality may be high, the intrinsic dimensionality (the number of dimensions that truly capture meaningful variations in the data) is often much lower. This can be seen in Figure \ref{}, where the ratio for real datasets is similar to that of much lower-dimensional synthetic data.

Studies on the distance metrics which are used to measure similarity between objects have been made, focusing particularly on the $l_p$ functional $||x|{|}_p$ defined as:

$$||x|{|}_p=(\sum _{i=1}^d{x}_i^p{)}^{1/p}$$

which is a norm for $p\ge 1$ and a quasinorm for $0<p<1$ since it violates the triangle inequality. Specifically on the quasinorms, a paper @aggarwalSurprisingBehaviorDistance2001 allegedly proved that using lower values of $p$, specifically fractional, helped to differentiate better the farthest and nearest distance of the points to the origin and thus reducing the distance concentration. Recently though it has been disproven @mirkesFractionalNormsQuasinorms2020, the results obtained in the first paper were deducted from a too small sample, so they are not statistically relevant and further it proved that smaller distance concentration does not mean better accuracy.